16 нуляля
Когда капитан вернулся, в руках у него был чертёж. Мы с Пи заглянули в него и только плечами пожали: из чего следует, что круг разделён на равновеликие части?
Но капитан словно бы и не заметил нашего недоверия. Он положил чертёж на бочку и стал объяснять.
- Перед вами круг с двумя взаимно перпендикулярными диаметрами. Каждый диаметр разделён на три равные части, а каждая из этих трёх равных частей, в свою очередь, представляет собой диаметр малого круга. Как видите, таких малых кругов в большом круге пять, и они совершенно одинаковы, то есть конгруэнтны. Известно, что если диаметр круга уменьшить, допустим, в три раза, то площадь круга уменьшится при этом в трижды три раза. Иными словами, площадь круга зависит от диаметра, взятого во второй степени (или, как говорят, от диаметра в квадрате). Отсюда следует, что площадь каждого из пяти малых кругов в девять раз меньше большого. Ведь три в квадрате равно девяти ( 3 * 3 = 9 ) !

Капитан перевёл дух и продолжал:
- Остаётся вычислить, чему равна площадь каждой из четырёх заштрихованных частей, заключённых между малыми кругами.
- Ну, это просто! - сейчас же выскочил я.- Если площадь большого круга принять за 9/9, то площадь всех пяти малых кругов составит 5/9, а на оставшиеся четыре части придётся 4/9. И части эти, само собой, тоже конгруэнтны.
- Отсюда ясно,- подытожил Пи,- что площадь каждой из заштрихованных частей также составляет 1/9 часть площади большого круга. Вот и выходит, что площадь большого круга разделена на девять равновеликих частей.
- Ура! - заорал я и завертелся на одной ножке.-Задача решена! Но вот как вам удалось сделать такой точный чертёж? Неужели только с помощью циркуля и линейки?
- О чертеже - потом,- сказал Единица.- Сперва разгородим коробку и расселим буянов, пока они не разбушевались снова.

В общем, не прошло и часа, как все девять тьфу-тьфу мирно спали в своих равновеликих отсеках. А во сне им, между прочим, цены нет! Я даже думаю, не отсюда ли пошла поговорка: "Хорош, когда спит!" Эти, во всяком случае, были так хороши, что штурман Игрек, несмотря на свои болячки, прямо влюбился в них. Он то и дело заглядывал в коробку, гладил то одного, то другого и даже называл милыми крошками, не забывая, впрочем, каждый раз сплюнуть через левое плечо: "Тьфу-тьфу, не сглазить!" Должно быть, на всякий случай...
Но капитан нашёл-таки способ отвлечь его: хватит ему умиляться! Пусть лучше объяснит нам, как сделать чертёж.
Сказать по правде, мы не очень-то обрадовались. Штурман у нас - полная противоположность капитану: горячий, нетерпеливый, к тому же до отказа нафарширован морскими словечками.
На сей раз к обычному его присловью прибавилось нечто новенькое.
- Бом-брам-фок! - заревел он.- Четыре взмаха циркулем, один - линейкой!
Мы уж подумали, что это очередное морское изречение, но штурман объяснил, что четыре взмаха циркулем и один линейкой - вот всё необходимое, чтобы сделать наш чертёж, а затем уж и вообще решить любую геометрическую задачу на построение.
Далее выяснилось, что для решения любой задачи на построение надо, в свою очередь, уметь решать две простейшие. И так как никто не начинает со второго (кстати, любимая поговорка кока), Игрек начал объяснять первую.
- Отдать концы! - гаркнул он и начертил на бумаге отрезок прямой.- Вот вам отрезок АВ. Требуется провести через его середину перпендикуляр. Что ж вы стоите? Выполняйте!
Легко сказать - выполняйте! А как? Сперва стали искать середину. Пи согнул было листок так, чтобы точки А п В совместились. Но бумага, как на грех, не просвечивала, и у него ничего не вышло.
- Бом-брам-фок! Штурман в сердцах швырнул бумажку за борт и достал большой деревянный циркуль с угольком вместо мела. Потом он вынул из кармана ещё один уголёк и провёл отрезок АВ прямо на палубе.
- Так-то! -сказал он ядовито.- Небось палубы пополам не перегнёшь!
- Уж конечно,- подтвердил я.- Но что же нам делать?
- Что за вопрос! - вскипел он.- А циркуль на что? Он засек циркулем две дужки из точки А и две - из точки В, а точки пересечения дужек обозначил буквами С - НАД отрезком АВ и Д - это уж ПОД ним.
- Вот вам и четыре взмаха циркулем,-сказал он.-Остаётся один взмах линейкой.
Тут он схватил линейку, соединил точки С и Д и посмотрел на нас взглядом полководца, выигравшего битву.
- То-то, бом-брам-фок! С одной задачей покончено. Переходим ко второй.
Он снова вычертил отрезок АВ, а повыше и чуть правее точки А поставил ещё одну точку - С.
- Задачка - проще некуда,-заявил он - Предлагается провести через точку С отрезок прямой, параллельный отрезку АВ. Ну-ка, раз, два, взяли!
На этот раз нам повезло: мы почему-то сразу догадались, что засечку следует делать из точки С. Только на какое расстояние раздвинуть циркуль? Оказалось, на такое, чтобы уголёк пересек отрезок АВ. Так мы и сделали, а точку пересечения обозначили буквой Д.
Один взмах был позади, и мы перешли к следующему: воткнули ножку циркуля в это самое Д и тем же раствором провели вторую дужку, которая пересекла отрезок АВ чуть правее. Эту точку обозначили буквой Е.
Потом иголка воткнулась в точку Е, а ножка циркуля описала дугу над отрезком и засекла дужку примерно на уровне точки С. Это был уже третий взмах. Оставался четвёртый, и последний.
Тут циркуль снова вонзился в точку С и тем же раствором провёл четвёртую дужку, которая пересеклась с предыдущей. Эту четвёртую точку окрестили буквой F.
- Циркуль отставить! Линейку на абордаж! - скомандовал Игрек и соединил отрезком прямой точки С и F. Потом он отшвырнул линейку и заорал: - Отбой! Отрезок CF параллелен АВ!
Теперь можно было приступать к нашему чертежу, но штурман спохватился, что не познакомил нас с ещё одной, совсем крохотной, но необходимой задачкой на построение.
- Так как эта третья задачка сводится к двум первым, будете решать сами,-сказал он и снова начертил отрезок АВ.- Требуется разделить данный отрезок на несколько одинаковых частей. Хоть на три.
Что и говорить, не сразу нам это далось, зато теперь-то уж мы знаем, как это делается.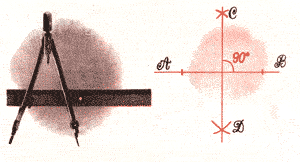

Берётся линейка, и к отрезку АВ из точки А проводится другой отрезок, любой длины и под любым острым углом. На нём, опять-таки от точки А, но уже с помощью циркуля откладываются ещё три совершенно одинаковых отрезка: АС, СД и ДЕ. Потом точки Е и В соединяются линейкой, а через точки Д и С проводятся отрезки, параллельные ЕВ (точки пересечения этих отрезков с АВ мы обозначили буквами К и F).
Так мы научились делить отрезок на равные части.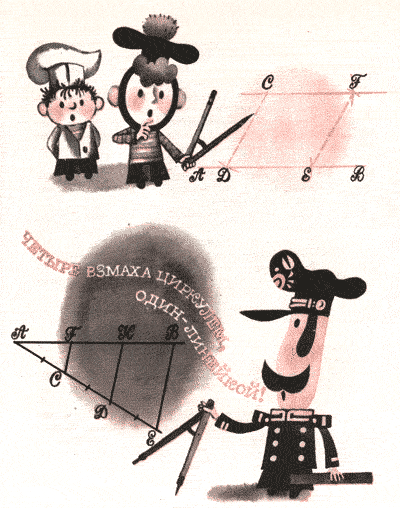

- Да, но почему эти отрезки равны между собой? Из чего это следует? Да из того, бом-брам-фок, что полученные нами треугольники AFC, АКД и ABE подобны! Ведь углы у них конгруэнтны! -загремел штурман.- А раз так - значит, стороны этих треугольников соответственно пропорциональны.
- Действительно,- согласился Пи.- Сторона АС относится к стороне АД как 1:2. Значит, как 1:2 относится также сторона AF к стороне АК. Отсюда AF=FK. По тем же причинам равны и отрезки FK и КВ.
Вот теперь можно было приступить к нашему чертежу.
Штурман начал с того, что вычертил окружность и предложил нам найти её центр.
- Что тут искать! - засмеялся я.- Центр там, где дырочка от циркуля.
- Э, нет, так дело не пойдёт! - сказал Игрек. Он достал блюдце, положил на палубу и обвёл угольком.
- Вот вам окружность без дырочки. Где у неё центр? Не знаете? А если я скажу, что диаметр, перпендикулярный к любой хорде, делит эту хорду пополам?
- Тогда другое дело! - обрадовался Пи.- Значит, надо провести какую-нибудь хорду, найти её середину, а затем провести через эту середину перпендикуляр. Так мы найдём диаметр круга. Теперь то же самое проделаем с диаметром, проведём через его середину перпендикуляр и получим, таким образом, ещё один диаметр. Ну, а точка пересечения двух диаметров и есть центр круга.
Тут мы принялись за дело, и через некоторое время на палубе появился чертёж капитана. Мы построили его сами, с помощью тех задач, с которыми нас познакомил штурман. При этом главную роль сыграли циркуль и линейка. Ну и, конечно же, голова! Без головы, как известно, ничего не делается. Даже глупости.