26 нуляля
Двенадцать суток - и ни одной стоянки! Всё на воде да на воде. Так я, чего доброго, разучусь ходить по суше...
- Ты что такой кислый? - спросил капитан.
- Соскучился по твёрдой почве,- буркнул я.
- Вот как! - прищурился он.- Но разве наш Фрегат стоит не на твёрдой почве?
Ну и шутник! Мы с коком расхохотались. Но оказалось, капитан вовсе не шутит.
- Ведь у нас Фрегат математический, а разве математика не та твёрдая почва, на которой развиваются самые разнообразные науки? - спросил он.- Начать с того, что возникла она как подспорье для астрономии, а это самая древняя и самая необходимая людям наука.
- Почему самая необходимая? - удивился я.- Астрономия изучает небесные тела, а люди-то живут на Земле.
- Но Земля - тоже небесное тело,- отвечал капитан,- стало быть, между ней и другими небесными телами существует взаимосвязь. Это-то и понял в глубокой древности человек, когда научился сопоставлять разные явления. Он увидел, что многое, происходящее на Земле, связано с тем, что происходит на небе. С движением Солнца, например. Человек заметил, что Солнце появляется всегда с одной стороны неба, а уходит в другую. В зависимости от этого на Земле становится то светло, то темно. По Солнцу человек научился отмерять сутки, отделять день от ночи. Точно так же по движению Солнца среди звёзд человек разделил свою жизнь на годы и месяцы. Звёзды помогали ему определять, когда следует ожидать разлива рек, когда начинать сев. Они не давали ему заблудиться в открытом море. Вот почему я сказал, что астрономия в далёкие времена была самой жизненно необходимой наукой. Но астрономия никогда не могла бы существовать без математики, так же, впрочем, как и другие науки. Постепенно математика проникала в самые разнообразные отрасли человеческой деятельности и знаний. Без неё невозможно было бы ни землемерие, ни судостроение, ни мореплавание, ни торговля. А в наше время без математики не обходится ни одна наука. Физика, химия, медицина, агрономия, философия, политическая экономия, статистика, логика... Даже языкознание! Словом,- заключил капитан,- теперь вы, надеюсь, согласны, что математика - поистине твёрдая почва любой науки, а стало быть, и всей нашей жизни.
- Вы забыли о кулинарии,- сказал Пи.-Хорошему кулинару тоже без математики не обойтись. Он должен точно рассчитать, сколько ему потребуется продуктов, чтобы вкусно и сытно накормить едоков.
- Да,- согласился капитан,- умение считать - великое дело. Но ещё важнее умение мыслить. Тем более, мыслить математически. Для примера предложу вам одну задачку. Что-то вроде небольшого домашнего задания. Не возражаете? Ну, мы, конечно, не возражали, и капитан тотчас приступил к делу.
- Представьте себе маленький шарик - ну, хотя бы горошину, которая опоясана ниточкой по экватору. Снимем эту ниточку (разумеется, мысленно) с горошины, выпрямим её и удлиним другой ниткой ровно на один метр. Далее уложим эту удлинённую нитку на столе так, чтобы она образовала окружность, а горошину поместим в центре окружности. А потом измерим зазор между ниткой и поверхностью горошины, и окажется, что он равен примерно 16 сантиметрам - уж поверьте мне на слово!
- Ну и что? - спросил я разочарованно.
- Сейчас увидишь,- сказал Единица.- Проделаем тот же опыт, но уже не с горошиной, а с земным шаром.
- Ого-го-го!-воскликнул Пи.- Земля - не горошина!
- А воображение на что? - спросил капитан.- Итак, мысленно снимем с Земли экватор, распрямим его. Получится приличная ниточка длиной этак в 40 миллионов метров. И удлиним её тоже ровно на один метр.
- Всего-навсего на один? - переспросил Пи.
- Всего-навсего. А дальше всё, как с горошиной: соединим концы удлинённого экватора, снова придадим ему форму окружности и наденем эту окружность на земной шар. Нам придётся её придерживать, чтобы она не свалилась, потому что между экватором и поверхностью земного шара появится зазор. И как вы думаете, какой?
- Наверное, его и в микроскоп не разглядишь,- предположил я.- Что такое один метр по сравнению с сорока миллионами!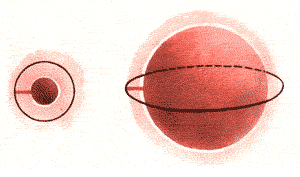

- Вот и видно, что математически ты мыслить не умеешь!- сказал капитан.- Расстояние между новым, удлинённым, и прежним экватором Земли будет то же, что и у горошины: около 16 сантиметров!
У нас от изумления глаза на лоб полезли.
- Чем зря таращиться, вспомнили бы лучше, каково отношение длины любой окружности к её диаметру, и подсчитали бы величину обоих зазоров,- посоветовал Единица.
Мы попросили его высказаться подробнее, но он стоял на том, чтобы мы решили задачу дома, по возвращении из плавания, для удобства проверив её на шаре диаметром в 100 сантиметров.
Но тут ему показалось, что одной задачи для домашнего задания мало, и он предложил нам вторую, о которой вспомнил, как видно, тут же, на месте.
Как раз в это время Фрегат наш вошёл в шлюз канала, и все мы стояли на корме, глядя, как медленно закрываются шлюзовые ворота. Сперва расстояние между створками было не менее 30 метров, потом оно стало постепенно уменьшаться. Вот уже просвет превратился в узкую длинную щёлку. Щёлка становилась всё меньше и меньше и наконец исчезла совсем. Да иначе и быть не могло! Так по крайней мере думал я.
Но капитан сказал, что веков двадцать пять назад в Древней Греции жил один мудрец по имени Зенон. Так вот, он утверждал, что можно сделать такую щель, которая не закроется, хотя и будет всё время уменьшаться. Эта-то задача и стала нашим вторым домашним заданием, которое мы с Пи записали от слова до слова:
"Однажды быстроногий Ахиллес решил состязаться в беге с черепахой. По условию он должен был бежать ровно в 10 раз быстрее её, но при этом дать ей 100 метров форы -то есть поставить её на 100 метров впереди себя. И вот состязание началось. Когда Ахиллес пробежал 100 метров, отделявших его от черепахи, её уже на этом месте не было: за это время она продвинулась вперёд на 10 метров. Ахиллес пробежал и эти 10 метров. Но за это время черепаха ушла вперёд ещё на 10 сантиметров. Так расстояние между ними всё время уменьшалось: то оно было равно одному сантиметру, потом одному миллиметру, одной десятой миллиметра, одной сотой, тысячной, миллионной, миллиардной... Черепаха всё время оказывалась впереди своего соперника. Хоть на самую малость, но впереди! Каким образом лучший бегун Греции не смог догнать самое медлительное существо на свете - черепаху?"
- Вы, конечно, понимаете, что Зенон малость ошибся,- сказал капитан, кончив диктовать.-А в чём его ошибка - потрудитесь разобраться сами.
- И потрудимся,-сказал я.-Но, во-первых, при чём здесь щель?
- Щель в данном случае - расстояние между Ахиллесом и черепахой, которое всё время уменьшается, но никогда не исчезнет.
- А это как раз то, чего я не понимаю во-вторых...

- ...и над чем тебе предстоит подумать дома,-закончил Единица.
И тут я разворчался. Зачем ломать голову над ошибками такого, с позволения сказать, мудреца?
Капитан задумчиво помолчал.
- Не торопись с выводами, юнга. Зенон, конечно, ошибся. Но он был, пожалуй, первым учёным, который представил себе бесконечно малую величину - то есть такую величину, которая всё время стремится к нулю, но никогда его не достигает. Вот и выходит, что Зенон как бы предвидел появление того самого научного понятия, которое много веков спустя, в XVII столетии, почти одновременно открыли два великих человека, англичанин Исаак Ньютон и немец Готфрид Вильгельм Лейбниц. А ведь это открытие означало целый переворот в науке! С помощью бесконечно малых величин учёным удалось решить многие, до тех пор нерешённые задачи. А главное, с тех пор практическое применение математики значительно расширилось. Кстати, изучение бесконечно малых величин остаётся одной из главных задач математики и доныне.
- Выходит, ошибки тоже иногда бывают полезными,- сказал Пи.
И тут мы с ним ни с того ни с сего развеселились и пустились куролесить вовсю: кувыркались по палубе, делали мостик и ещё невесть что.
- Да вы, я вижу, настоящие акробаты,- добродушно рассмеялся капитан.- Раз так, давайте проведём небольшое спортивно-математическое состязание.
В руках у него непонятным образом появилась мягкая широкополая шляпа из белоснежного фетра, на которой легонько трепыхалось курчавое страусовое перо. Чудесная была шляпа! Мы так и впились в неё глазами и очень обрадовались, когда узнали, что капитан собирается нам её подарит?, Правда, для этого надо сперва решить одну пустяковую задачку.
Сказав это, капитан повёл нас вниз, в большой зал кают-компании, и предложил тянуть жребий: кому из нас быть абсциссой, кому - ординатой. Ну, мне досталась абсцисса, а Пи, само собой, ордината. А потом капитан объяснил, что на полу, под ковром, находится кнопка звонка, и наша задача отыскать её.
Если принять за оси координат взаимно перпендикулярные кромки ковра, то координаты этой кнопки в сумме равны одиннадцати метрам. При этом абсцисса на 10 метров больше ординаты. Остаётся решить, какова длина абсциссы и какова длина ординаты. После этого каждый из нас должен на руках пробежать своё расстояние вдоль кромок ковра, а оттуда и до пересечения перпендикуляров, восстановленных из этих точек. И если мы рассчитали правильно, то обязательно попадём туда, где спрятана кнопка. Прозвучит звонок -и дело в шляпе!
Ну, мы посовещались немного, а потом встали на руки и побежали вдоль кромок. Я пробежал десять метров, Пи -один. Потом мы пробежали по перпендикулярам до точки нашего взаимного пересечения и... никакого звонка не последовало. Как же так? Всё как будто верно. Ведь сумма координат равна одиннадцати, а это и есть 10 + 1 !
- Так-то так,- сказал капитан.- Сумма у вас, действительно, правильная. Но вы забыли, что путь одного из вас должен быть на десять метров больше, чем путь другого, а у вас он больше только на девять метров ( 10 - 1 = 9 ). Выходит, с задачей вы пока не справились. Так что пусть уж она будет вашим третьим домашним заданием.
После этого мы с позором удалились, а шляпа -белоснежная мягкая фетровая шляпа - так и осталась у капитана. Неужто не найдётся на свете никого, кто бы помог нам её заполучить?