3 нуляля
Управившись со своими делами, мы с коком вышли на палубу. Капитан был уже там и рассматривал что-то в бинокль. Зюйд-зюйд-ост! - приветствовал он нас.- Фрегат идёт вдоль Берега Точных Доказательств. Здесь надо вести судно особенно осторожно: всюду подстерегают подводные камни. Один неумелый манёвр, и можно утонуть в море Ошибок. Впрочем, штурман Игрек моряк опытный...
-Хотел бы я знать, что это такое - Берег Точных Доказательств? - шепнул я на ухо Пи.
Но капитан всё равно услышал и протянул нам что-то вроде значка. Оказалось, однако, что это не значок, а герб Берега Точных Доказательств. На нём были всякие геометрические фигуры и надпись: "Слава точным и кратким доказательствам!"
Да, это вам не бухта Аксиома, где ничего доказывать нельзя! Здесь не только можно, а и нужно. Но капитан сказал, что без аксиом и тут не проживёшь. Потому что без них ничегошеньки не докажешь. Ни одной теоремы!
Опять новое слово! Теорема. Мы спросили, что это такое, и узнали, что "теорема" - слово греческое, и означает оно "обдумывание". Чтобы доказать теорему, надо много думать.
-В таком случае доказывать теоремы - дело трудное,- сказал я.
Трудное,- согласился капитан,- но вполне возможное. Если только думать логически, то есть последовательно. Умение рассуждать последовательно необходимо каждому, а математику - особенно.
Мы попросили капитана доказать какую-нибудь теорему. Он нарисовал два прямоугольных треугольника (теперь-то я знаю, что это за штука!) и велел запомнить, что точки, где сходятся стороны треугольника, называются вершинами. Таких вершин у треугольника, само собой разумеется, три. Он обозначил их латинскими буквами. В одном треугольнике- большими (А, В, С), в другом - маленькими (а, в, с).
-Эти два треугольника замечательны тем, что меньшие и большие их катеты одинаковы по длине. Требуется доказать, что в этом случае треугольники конгруэнтны.
Как он сказал? Кон-гру... Ну и словечко!
Мы с Пи так хохотали, что чуть в воду не свалились!
-В чём дело? - растерялся капитан.- По-моему, я не сказал ничего смешного.
Лицо у него было такое обиженное, что нам сразу расхотелось смеяться, зато очень захотелось узнать, что за слово такое.
Тут капитан подобрел и спросил, известно ли нам, что такое равенство двух фигур?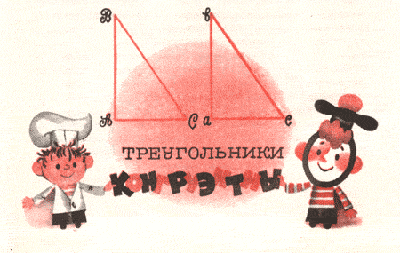

- Уж конечно, известно,- бодро заявил я.- Это когда две фигуры равны между собой.
Тут я с капитаном поменялся ролями: на сей раз хохотал он, а обижался я. Но потом он признал, что, в общем-то, объяснение у меня правильное. Только вместо "равны между собой" теперь говорят коротко и ясно - конгруэнтны.
Вот так коротко! Вот так ясно! Да этакого натощак и не выговоришь!
Но капитан сказал, что это разве с непривычки не выговоришь, а вообще-то слово как слово. По-латыни - "совпадение". Если две геометрические фигуры или линии при наложении друг на друга полностью совпадают, значит, они конгруэнтны.
После этого спорить было бесполезно, и мы перешли к теореме.
- Займёмся доказательством,- предложил капитан.
- Ну, это просто,- сказал Пи.- Вырежем из бумаги два прямоугольных треугольника, у которых меньшие и большие катеты одинаковы, наложим один на другой, и если треугольники совпадут, стало быть, они конру... конгруэнтны.
- Не доказательство, а кит знает что! - проворчал капитан.- Во-первых, нам может только показаться, что треугольники одинаковы. Ведь ножницы, циркуль, линейка, да и глаз человеческий - всё это инструменты далеко неидеальные. Во-вторых, если даже допустить, что треугольники действительно одинаковы и совпали в точности, то мы докажем лишь то, что совпали именно эти два треугольника. А теорема должна быть справедливой для всех прямоугольных треугольников с соответственно конгруэнтными катетами.
- Что же делать? - растерялся я.
Что? - Капитан прищурился и пососал свою трубку.- Прежде всего, отказаться от бумажных треугольников и заменить их воображаемыми. Ну и, конечно, рассуждать логически. Итак, у нас есть два воображаемых треугольника, у которых катеты соответственно конгруэнтны. Допустим, что я мысленно накладываю вершину прямого угла одного треугольника на вершину прямого угла второго. То есть точку А на точку а. А потом накладываю друг на друга два конгруэнтных катета. Совпадут концы этих катетов - точки В и в?
- Совпадут,- ответил Пи.- Ведь катеты конгруэнтны…
- Верно. Теперь допустим, что два катета крепко-накрепко склеились. Належатся друг на друга два других катета?
- Ясно, належатся,- ответил я.- Углы между катетами у обоих треугольников прямые - по 90 градусов.
- И длины у катетов тоже одинаковые,- добавил Пи.
- А вы делаете успехи,- заметил капитан.- Итак, логика помогла нам выяснить, что и два других катета обоих треугольников накрепко склеились. Остаётся установить, совпали ли гипотенузы.
Мы с Пи понимали, что гипотенузы обязательно совпадут, но капитан потребовал, чтобы мы это до-ка-за-ли! Да, нелёгкая это работа - из болота тащить бегемота! Хорошо ещё, капитан задал наводящий вопрос: все ли вершины треугольника совпали?
- Все! - заявил Пи.
- Значит,- сообразил я,- совпали и гипотенузы ВС и вс!
-Ой, ли? А из чего это следует? - прищурился капитан. Из чего? Ах я чудак этакий! Да из аксиомы! Из аксиомы о том, что через две точки можно провести только одну прямую!
-Логично,- кивнул капитан.- Теперь теорема доказана: треугольники в точности наложились один на другой. Стало быть, они кон-гру-энт-ны!
-Ура! Да здравствуют аксиомы! - закричали мы с коком. Вот какая у нас с ним конгруэнция!